Modularity详解
文章目录
Modularity
模块度是一种常用的衡量节点分组质量的标准。模块度越高说明所检测到的社团越符合“内紧外松”的特征,分组质量越好。
定义
$Q=\displaystyle \frac{1}{2m}* \displaystyle \sum_{ij}{[A_{ij}-\displaystyle \frac{k_{i}*k_{j}}{2m}]}δ(C_i,C_j)$
$Q$ 就是模块度,模块度越大则表明社区划分效果越好。 $Q$ 值的范围在[-0.5,1),论文表示当 $Q$ 值在0.3~0.7之间时,说明聚类的效果很好。 现在假设有 $x$ 个节点,每个节点都代表一个输入,并且我们已经将这些输入划分为了 $N$ 个社区,节点彼此之间共有 $m$ 个连接。$i$ 和 $j$ 是 $x$ 中的任意两个节点,当两个节点直接相连时 $A_{ij}=1$,否则 $A_{ij}=0$。$k_i$ 代表的是节点 $i$ 的度,度是图论的基础知识,从一个节点出发有几个边,我们就说这个节点的度是多少。很容易理解,这里的 $2m$ 实际就是整个图中的度(每个节点都计算一次度,那么每条边对应两个节点,所以要乘以2)。$δ(C_i,C_j)$ 是用来判断节点 $i$ 和 $j$ 是否在同一个社区内,在同一个社区内$δ(C_i,C_j)=1$,否则 $δ(C_i,C_j)=0$。
其他定义:
$ Q= \displaystyle \sum_{i}(e_{ii}-a_{i}^2) = \displaystyle \sum_{i}e_{ii}-\displaystyle \sum_{i}a_{i}^2$
$e_{ij}$ 表示连接社团 $i$ 和社团 $j$ 的边的数目占总边数的比例。当 $i==j$ 时表示的是社团 $i$ 内部的边占总边数的比例
$a$ 为 $e_{ij}$ 的行和,$a_{i} = \displaystyle \sum_{j}e_{ij}$ ,它表示跟社团 $i$ 中边占总边数的比例(未完全在社区内的边为1/2)
模块度计算示例
完整图如下:
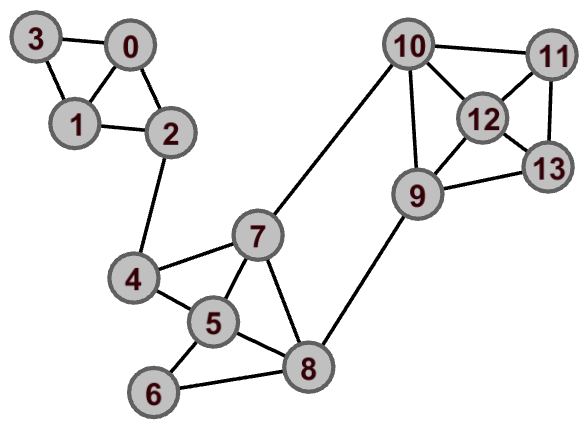
划分结果如下:

对其模块度进行计算:
社团内节点有节点14个总计关系数 $m = 23$ , 矩阵 $e$ 为:
| 社团 | 社团1 | 社团2 | 社团3 |
|---|---|---|---|
| 社团1 | $\displaystyle \frac {5}{23}$ | $\displaystyle \frac{1}{2} *\displaystyle \frac{1}{23}$ | $\displaystyle \frac{1}{2} *\displaystyle \frac{0}{23}$ |
| 社团2 | $\displaystyle \frac{1}{2} *\displaystyle \frac{1}{23}$ | $\displaystyle \frac {7}{23}$ | $\displaystyle \frac{1}{2} *\displaystyle \frac{2}{23}$ |
| 社团3 | $\displaystyle \frac{1}{2} *\displaystyle \frac{0}{23}$ | $\displaystyle \frac{1}{2} *\displaystyle \frac{2}{23}$ | $\displaystyle \frac {8}{23}$ |
计算:
$Q = \displaystyle \sum_{i}e_{ii}-\displaystyle \sum_{i}a_{i}^2$
$Q = \displaystyle \frac{5}{23}+\displaystyle \frac{7}{23}+\displaystyle \frac{8}{23} - (\displaystyle \frac{5}{23} + \displaystyle \frac{1}{2} *\displaystyle \frac{1}{23} +\displaystyle \frac{1}{2} *\displaystyle \frac{0}{23})^2 - (\displaystyle \frac{1}{2} *\displaystyle \frac{1}{23}+\displaystyle \frac{7}{23}+\displaystyle \frac{1}{2} *\displaystyle \frac{2}{23})^2-(\displaystyle \frac{1}{2} *\displaystyle \frac{0}{23}+\displaystyle \frac{1}{2} *\displaystyle \frac{2}{23}+\displaystyle \frac{8}{23})^2$
$Q = \displaystyle \frac{5}{23}+\displaystyle \frac{7}{23}+\displaystyle \frac{8}{23} -(\displaystyle \frac{11}{46})^2-(\displaystyle \frac{17}{46})^2-(\displaystyle \frac{18}{46})^2$
$Q = \displaystyle \frac{1106}{2116} \approx 0.52268$
文章作者 玉面蟾蜍
上次更新 2022-04-15 Fri
