KNN算法详解

KNN算法是一种非参数分类算法(不需要训练参数)，隶属于有监督学习，其核心思想为：“近朱者赤近墨者黑”

定义

KNN（K- Nearest Neighbor）法即K最邻近法：如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别

如下图所示：

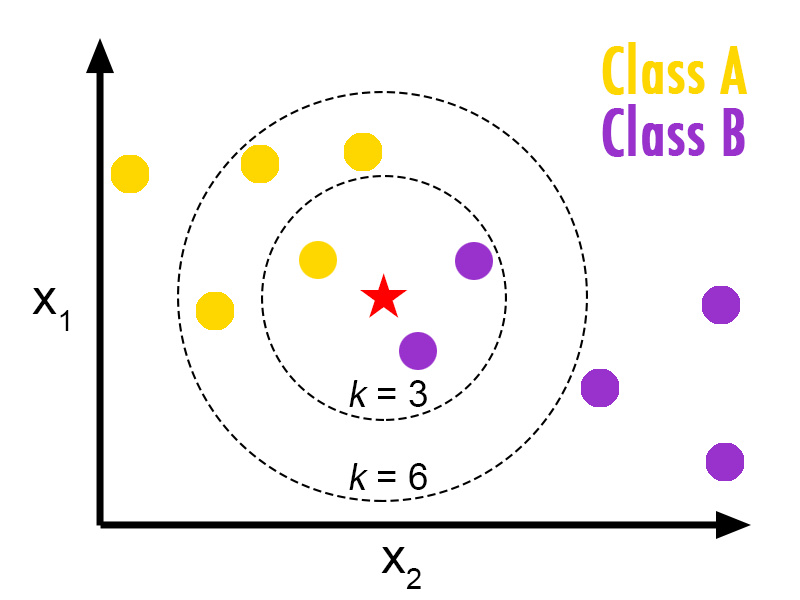
当KNN的K定义为3，则在五角星最近的3个点内，分类为B的点最多，则五角星的分类为B

当KNN的K定义为6，则在五角星最近的6个点内，分类为A的点最多，则五角星的分类为A

三要素

距离度量算法：一般使用的是欧氏距离。也可以使用其他距离：曼哈顿距离、切比雪夫距离、闵可夫斯基距离等。各种距离方法见链接

k值的确定：k值越小，模型整体变得越复杂，越容易过拟合。通常使用交叉验证法来选取最优k值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

# talk is cheap show me the code

# 导入算法包
from random import choice
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import KFold, StratifiedKFold

# 预设进行10段交叉验证
N = 10

#采用鸢尾花数据集： X 为特征向量，y 为标签向量
iris = datasets.load_iris()
X = iris['data']
y = iris['target']

# 定义候选值，对于二分类模型，通常选取20以内的奇数
k_candidate = [i for i in range(1,20) if i%2!=0]
# 进行10折交叉验证，返回的是训练集和验证集的下标
# KFold,StratifiedKFold中选择StratifiedKFold是考虑数据分布，选择KFold为考虑均分
# fk = KFold(n_splits=N, shuffle=True, random_state=521)
fk = StratifiedKFold(n_splits=N, shuffle=True, random_state=521)


# 预设准确率
maximum_accuracy = 0
# 预设best的k
best_k = choice(k_candidate)


# 遍历所有的候选值
for k in k_candidate:
    # 记录10段的准确率之和 
    count_accuracy = 0
    # 遍历10段的数据集
    # for train_index,valid_index in fk.split(X):
    for train_index,valid_index in fk.split(X,y):
        # 实例化KNN模型
        clf = KNeighborsClassifier(n_neighbors=k)
        # 训练模型
        clf.fit(X[train_index], y[train_index])
        # 统计累计准确率
        count_accuracy = count_accuracy + clf.score(X[valid_index], y[valid_index])
    # 计算KNN模型的K值为k时的平均准确率值
    count_accuracy = count_accuracy/N
    print('平均准确率为：%.2f' % count_accuracy)
    # 判断平均准确率值是否大于目前最大的准确率值
    if count_accuracy > maximum_accuracy:
        # 将平均准确率值替代原先最大的准确率值
        maximum_accuracy = count_accuracy
        # 将目前的K值替换原先最好的K值
        best_k = k
    print('当前最好的K值为：%d'%best_k,"当前最大的准确率值为：%.2f"%maximum_accuracy)
    print("*"*60)
print('评估最合适的K值为：%d'%best_k,"其准确率为：%.2f"%maximum_accuracy)

分类决策：一般使用多数表决，即在 k 个临近的训练点钟的多数类决定输入实例的类。可以证明，多数表决规则等价于经验风险最小化

假设我们的损失函数为 0,1损失函数 - 分类错误$loss+1$，分类函数为 $f(z)$

误分类概率：$P(y\neq f(z)) = 1 -P(y=f(z))$

误分类率：$\frac {1} {k}\displaystyle \sum_{x_i \in N_k(z)}{I(y_i\neq c_j)} = 1-\frac{1}{k}\displaystyle \sum_{x_i \in N_k(z)}{I(y_i= c_j)}$

因此为了使误分类率最小，就要最大化：$ \frac{1}{k}\displaystyle \sum_{x_i \in N_k(z)}{I(y_i= c_j)}$

而使之最大化，则就应使得$\pmb c_j$为$\pmb N_k(z)$中的大多数表达，即为多数表决规则(Vote)

核心问题

KNN是一种惰性机器学习方法：

优点：

  • 天生支持增量学习（不需要训练，没有增量拓展的麻烦事儿）
  • 可以用于非线性分类
  • 能对超多变形的复杂决策空间建模
  • 在数据量不多但数据代表性较强时，kNN分类效果较好

缺点：

  • 计算开销大
  • 可解释性不强
  • 样本不平衡的时候，对稀有类别的预测准确率低

针对部分数据（特征空间维度大，数据容量大），可使用KD Tree加速检索过程。

kd Tree 是一种平衡二叉树，目的是实现对 k 维空间的划分。

kd树构造

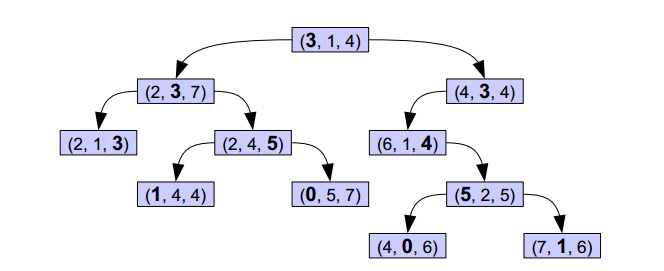
上图的树就是一棵KDTree，形似二叉搜索树，其实KDTree就是二叉搜索树的变种。这里的K = 3(维度).

首先来看下树的组织原则。将每一个元组按0排序（第一项序号为0，第二项序号为1，第三项序号为2），在树的第n层，第 n%3 项被用粗体显示，而这些被粗体显示的树就是作为二叉搜索树的key值，比如，根节点的左子树中的每一个节点的第一个项均小于根节点的的第一项，右子树的节点中第一项均大于根节点的第一项，子树依次类推。

对于这样的一棵树，对其进行搜索节点会非常容易，给定一个元组，首先和根节点比较第一项，小于往左，大于往右，第二层比较第二项，依次类推。

kd树检索

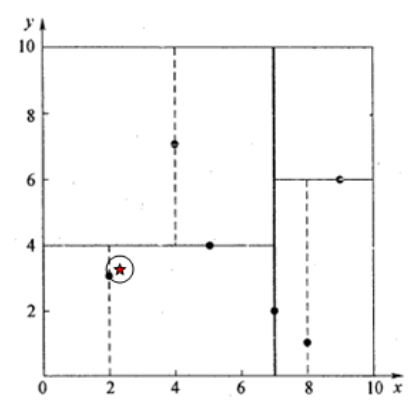
假设我们的k-d tree通过样本集{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}创建的。 我们来查找点(2.1,3.1)，在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2), (5,4), (2,3)>，从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141 （欧氏距离）； 然后回溯至(5,4)，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆，并不和超平面y=4相交，如下图，所以不必跳到结点(5,4)的右子空间去搜索，因为右子空间中不可能有更近样本点了。 于是在回溯至(7,2)，同理，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆并不和超平面x=7相交，所以也不用跳到结点(7,2)的右子空间去搜索。 至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。

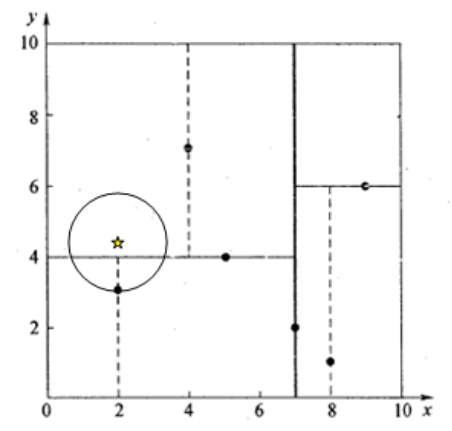
再举一个稍微复杂的例子，我们来查找点(2,4.5)，在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)，然后search_path中的结点为<(7,2), (5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202； 然后回溯至(5,4)，以(2,4.5)为圆心，以dist=3.202为半径画一个圆与超平面y=4相交，如下图，所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中，现在search_path中的结点为<(7,2), (2, 3)>；另外，(5,4)与(2,4.5)的距离为3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。 回溯至(2,3)，(2,3)是叶子节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)，dist更新为(1.5) 回溯至(7,2)，同理，以(2,4.5)为圆心，以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。 至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

应用场景

数据敏感度

1、对数据没有假设，准确度高，对异常点不敏感

2、样本不平衡的时候，对稀有类别的预测准确率低

实际应用

经常在stacking中与其他模型组合使用，例如采用svm的特征为KNN加权

面试常见问题

1、不平衡的样本可以给KNN的预测结果造成哪些问题，有没有什么好的解决方式？

输入实例的K邻近点中，大数量类别的点会比较多，但其实可能都离实例较远，这样会影响最后的分类。 可以使用权值来改进，距实例较近的点赋予较高的权值，较远的赋予较低的权值。

2、为了解决KNN算法计算量过大的问题，可以使用分组的方式进行计算，简述一下该方式的原理。

先将样本按距离分解成组，获得质心，然后计算未知样本到各质心的距离，选出距离最近的一组或几组，再在这些组内引用KNN。本质上就是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本，该方法比较适用于样本容量比较大时的情况。

3、KD树建立过程中切分维度的顺序是否可以优化？

先对各个维度计算方差，选取最大方差的维度作为候选划分维度(方差越大，表示此维度上数据越分散)；对split维度上的值进行排序，选取中间的点为node-data；按照split维度的node-data对空间进行一次划分；对上述子空间递归以上操作，直到空间只包含一个数据点。分而治之，且循环选取坐标轴。从方差大的维度来逐步切分，可以取得更好的切分效果及树的平衡性。

4、KD树每一次继续切分都要计算该子区间在需切分维度上的中值，计算量很大,有什么方法可以对其进行优化？

算法开始前，对原始数据点在所有维度进行一次排序，存储下来，然后在后续的中值选择中，无须每次都对其子集进行排序，提升了性能。

5、KNN与K-means的区别

KNN

  • 分类算法
  • 监督学习
  • 数据集是带Label的数据
  • 没有明显的训练过程，基于Memory-based learning
  • K值含义 - 对于一个样本X，要给它分类，首先从数据集中，在X附近找离它最近的K个数据点，将它划分为归属于类别最多的一类

K-means

  • 聚类算法
  • 非监督学习
  • 数据集是无Label，杂乱无章的数据
  • 有明显的训练过程
  • K值含义- K是事先设定的数字，将数据集分为K个簇，需要依靠人的先验知识

Kmeans算法的缺陷：

  • 聚类中心的个数K 需要事先给定，但在实际中这个 K 值的选定是非常难以估计的，很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适
  • Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果。（可以使用Kmeans++算法来解决）

参考：

机器学习面试题之KNN

KNN与kdTree+Python实现

详解KD Tree