决策树算法

决策树(Decision Tree)是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。

决策树模型定义

形式上：决策树是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型

内部节点(internal node)：表示一个特征维度或一个属性

叶节点：表示一个类本质上：是if-then的规则集合；也可以被认为是定义在特征空间与类空间上的条件概率分布

1、if-then的规则集合

决策树的路径或其对应的if-then规则集合具有一个重要的性质：互斥且完备

即每一个实例都被一条路径或一条规则所覆盖，而且只被一条路径或一条规则所覆盖

2、定义在特征空间与类空间上的条件概率分布

决策树还是给定特征条件下，类别的条件概率分布的一种退化表示（非等效）。

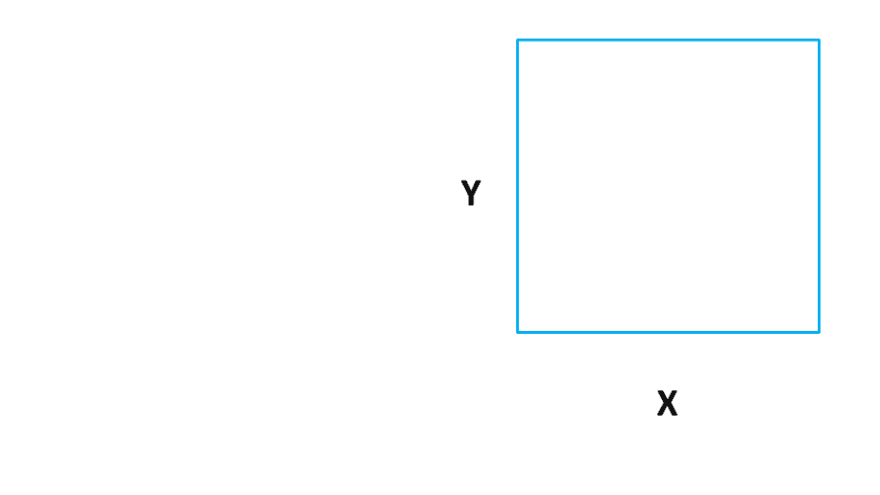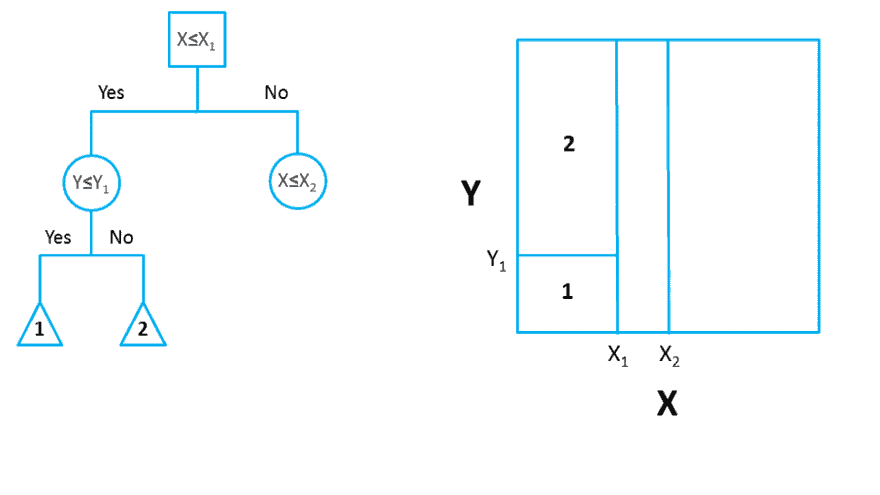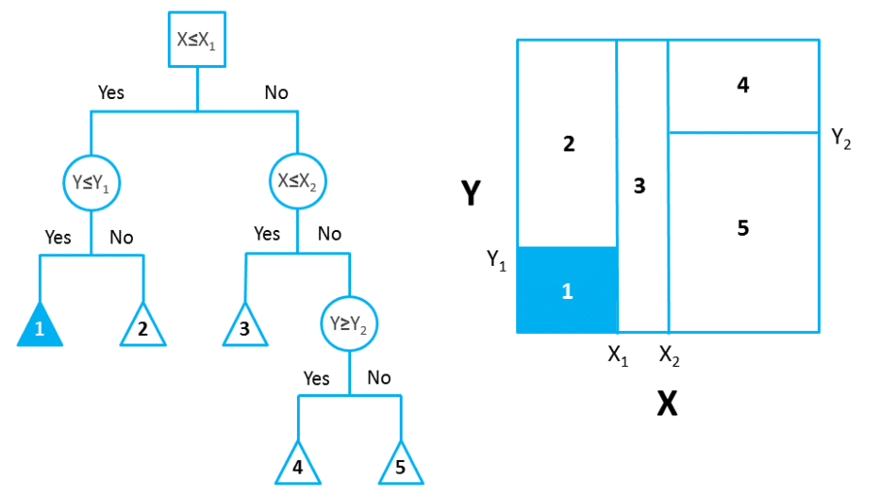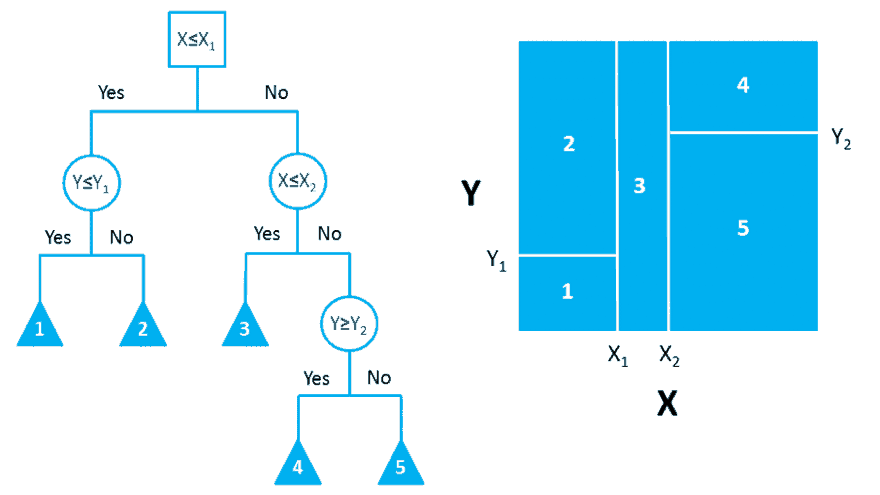
该条件分布定义在特征空间的划分上（每个划分代表一个条件），特征空间被划分为互不相交的单元，每个单元定义一个类的概率分布就构成了一个条件概率分布。

决策树所表示的整体条件概率分布由各个单元在给定条件下类的条件概率分布组成，决策树的每条路径对应于划分中的一个单元。给定实例的特征X，一定落入某个划分，决策树选取该划分里最大后验概率对应的类（期望风险最小化）作为结果输出。这点上和朴素贝叶斯和KNN的决策思想是一致的

与KD树区别

1、KD树轮递归选择方差最大的特征S作为区分标准，以S的中位数作为根节点；而决策树采用信息论方法

2、KD树特征重复使用；决策树仅用一次

3、KD树目的是为了找近邻；决策树是为了分类

基于特征选择决策树可分三大类

ID3

ID3 算法是建立在奥卡姆剃刀（用较少的东西，同样可以做好事情）的基础上：越是小型的决策树越优于大的决策树。

奥卡姆剃刀：若无必要，勿增实体；在所有符合实验数据的模型中，简单的模型优于复杂模型。

特征选择依据：信息增益

熵：在信息论里面，熵是对不确定性的测量；熵越高，则能传输越多的信息，熵越低，则意味着传输的信息越少。熵的公式 $H(X) = -\displaystyle \sum_{i}{P(x_i)logP(x_i)}$ $P$ 表示 $x$ 的概率质量

条件熵：在一个条件下，随机变量的不确定性。

信息增益：熵 - 条件熵。表示在一个条件下，信息不确定性减少的程度。

特征 $A$ 与数据集 $D$ 间的信息增益定义为：集合 $D$ 的经验熵 $H(D) $ 与 $A$ 特征给定条件下的经验条件熵 $H(D|A)$ 的差值。$g(D,A) = H(D) - H(D|A)$

$H(D)$ 表示数据集的不确定性，而 $H(D|A)$ 表示在 $A$ 确定的条件下数据集的不确定性，差值表示在特征 $A$ 下使得数据集不确定减少的程度，即每次选择使得 $g(D, A)$ 最大的特征 $A$

ID3的问题

ID3 没有剪枝策略，容易过拟合；

信息增益准则对可取值数目较多的特征有所偏好，类似“编号”的特征其信息增益接近于 1；

只能用于处理离散分布的特征；

没有考虑缺失值。

C4.5

针对ID3对特征数目的偏重缺陷，引入信息增益率来作为分类标准

$g_{ratio}(D, A) = \displaystyle \frac {g(D,A)}{H_A(D)}$ 其中 $H_A(D) = -\displaystyle \sum_{i=1}^{n} \displaystyle \frac{|D_i|}{|D|}log\displaystyle \frac{|D_i|}{|D|}$

信息增益率对可取值较少的特征有所偏好（分母越小，整体越大），因此 C4.5 并不是直接用增益率最大的特征进行划分，而是使用一个启发式方法：先从候选划分特征中找到信息增益高于平均值的特征，再从中选择增益率最高的。

C4.5的问题

C4.5 用的是多叉树，用二叉树效率更高；

C4.5 只能用于分类；

C4.5 使用的熵模型拥有大量耗时的对数运算，连续值还有排序运算；

C4.5 在构造树的过程中，对数值属性值需要按照其大小进行排序，从中选择一个分割点，所以只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时，程序无法运行。

CART

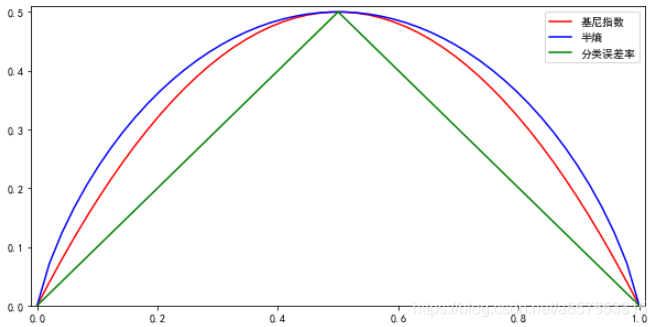
熵模型拥有大量耗时的对数运算，基尼指数在简化模型的同时还保留了熵模型的优点。基尼指数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。这和信息增益（率）正好相反。

$Gini(D) = \displaystyle \sum_{k=1}^{K}\displaystyle \frac{|C_k|}{|D|}(1-\displaystyle \frac{|C_k|}{|D|}) = 1-\displaystyle \sum_{k=1}^K(\displaystyle \frac{|C_k|}{|D|})^2$

学习过程

以周老师的西瓜为例

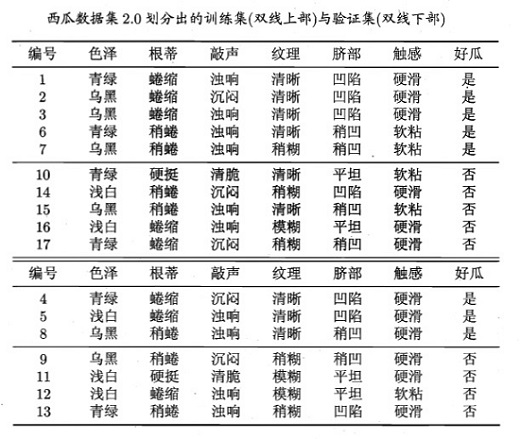
使用信息增益计算：

决策树学习策略

决策树学习用损失函数来表达对训练数据的拟合以及泛化能力的目标，所以，决策树学习的损失函数通常是正则化的极大似然估计。决策树学习的策略是以损失函数为目标函数的最小化，这对应于结构风险最小策略。

决策树无法一步到位得到整个模型的结构！通常使用贪心的最优化算法

由于贪心算法的性质，导致在训练集中效果较好，但测试集就不好说了。根据结构化风险最小策略思想，我们需要对已生成的树自上而下进行剪枝，将树变得更简单（奥卡姆剃刀原则），从而使它具有更好的泛化能力

决策树剪枝

在决策树学习中将已生成的树进行简化的过程称为剪枝 (Pruning)。具体地，剪枝从已生成的树上裁掉一些子树或叶结点，并将其根结点或父结点作为新的叶结点，从而简化分类树模型。

剪枝分为两种：

预剪枝（pre-pruning）：预剪枝就是在构造决策树的过程中，先对每个结点在划分前进行估计，若果当前结点的划分不能带来决策树模型泛华性能的提升，则不对当前结点进行划分并且将当前结点标记为叶结点。

后剪枝（post-pruning）：后剪枝就是先把整颗决策树构造完毕，然后自底向上的对非叶结点进行考察，若将该结点对应的子树换为叶结点能够带来泛华性能的提升，则把该子树替换为叶结点。

决策树的剪枝往往通过极小化决策树整体的损失函数 (Loss Function) 或代价函数 (Cost Function) 来实现。设树 $T$ 的叶结点个数为 $|T|$，$t$ 是树 $T$ 的叶结点，该叶结点有 $N_{t}$ 个样本点，其中 k 类的样本点有 $N_{tk}$ 个，k=1,2,⋯ ,K，$H_{t}(T)$ 为叶结 t 点上的经验熵，$α≥0$ 为参数，则决策树学习的损失函数可以定义为: $C_{α}(T)=\sum_{t=1}^{ | T |}N_{t}H_{t}(T)+α | T |$

其中经验熵为： $H_{t}(T)=-\sum_{k}\frac{N_{tk}}{N_{t}}\log \frac{N_{tk}}{N_{t}}$

在损失函数中，记：$C(T)=\sum_{t=1}^{\left | T \right |}N_{t}H_{t}(T)=-\sum_{t=1}^{\left | T \right |}\sum_{k=1}^{K}N_{tk}\log \frac{N_{tk}}{N_{t}}$

这时有： $C_{a}(T)=C(T)+α|T|$

$C(T)$ 表示模型对训练数据的预测误差，即模型和训练数据的拟合程度，$|T|$ 表示模型复杂度，参数 $α⩾0$ 控制两者之间的影响。

剪枝，就是当 $α$ 确定时，选择损失函数最小的模型，即损失函数最小的子树。可以看出，决策树生成只考虑了通过提高信息增益对训练数据进行更好的拟合。而决策树剪枝通过优化损失函数还考虑了减小模型复杂度。决策树生成学习局部的模型，而决策树剪枝学习整体的模型。

决策树优缺点

决策树优点：

决策树易于理解和实现. 人们在通过解释后都有能力去理解决策树所表达的意义。

对于决策树，数据的准备往往是简单或者是不必要的 . 其他的技术往往要求先把数据一般化，比如去掉多余的或者空白的属性。

能够同时处理数据型和常规型属性。其他的技术往往要求数据属性的单一。

在相对短的时间内能够对大型数据源做出可行且效果良好的结果。

对缺失值不敏感

可以处理不相关特征数据

效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度。

决策树缺点：

对连续性的字段比较难预测。

对有时间顺序的数据，须要不少预处理的工做。

当类别太多时，错误可能就会增长的比较快。

通常的算法分类的时候，只是根据一个字段来分类。

在处理特征关联性比较强的数据时表现得不是太好

参考：

决策树

DT算法详解

文章目录