DBSCAN算法详解

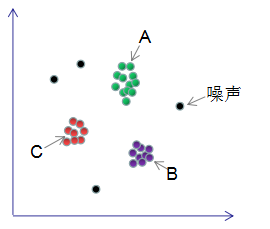
DBSCAN是基于密度空间的聚类算法，在机器学习和数据挖掘领域有广泛的应用，其聚类原理通俗点讲是每个簇类的密度高于该簇类周围的密度，噪声的密度小于任一簇类的密度。如下图簇类ABC的密度大于周围的密度，噪声的密度低于任一簇类的密度，因此DBSCAN算法也能用于异常点检测。

DBSCAN的样本点组成

DBSCAN算法处理后的聚类样本点分为：核心点(core points)，边界点(border points)和噪声点(noise)，这三类样本点的定义如下：

核心点：对某一数据集D，若样本p的 $\varepsilon-$ 领域内至少包含$MinPts$个样本（包括样本p），那么样本p称核心点。

即：$N_{\varepsilon}(p)\geq MinPts$

称p为核心点，其中 $\varepsilon-$ 领域 $N_{\varepsilon}(p)$ 的表达式为：

$N_{\varepsilon}(p) = \{q \in D|dist(p,q) \leq \varepsilon \}$

边界点：对于非核心点的样本 $b$，若 $b$ 在任意核心点 $p$ 的领 $\varepsilon-$ 域内，那么样本 $b$ 称为边界点。

即：

$p、b$ 分别为核心点与非核心点

$b \in N_{\varepsilon}(p) $ 称 $b$ 为边界点

噪声点：对于非核心点的样本n，若n不在任意核心点p的 $\varepsilon-$ 领域内，那么样本n称为噪声点。

即：

$p、n$ 分别为核心点与非核心点

$n \notin N_{\varepsilon}(p) $ 称 $b$ 为噪声点。

假设$MinPts=4$，如下图的核心点、非核心点与噪声的分布：

DBSCAN算法原理

DBSCAN算法划分数据集D为核心点，边界点和噪声点，并按照一定的连接规则组成簇类。介绍连接规则前，先定义下面这几个概念：

密度直达（directly density-reachable）：若 $q$ 处于 $p$ 的 $\varepsilon-$ 邻域内，且 $p$ 为核心点，则称 $q$ 由 $p$ 密度直达；

密度可达（density-reachable）：若 $q$ 处于 $p$ 的 $\varepsilon-$ 邻域内，且 $p$ ，$q$ 均为核心点，则称 $q$ 的邻域点由 $p$ 密度可达；

密度相连（density-connected）：若 $p $，$q$ 均为非核心点，且 $p$ ，$q$ 处于同一个簇类中，则称 $q$ 与 $p$ 密度相连。

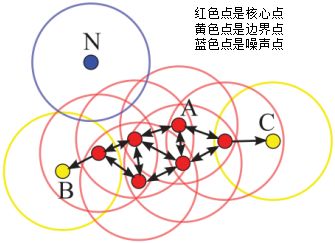
下图给出了上述概念的直观显示（$MinPts=4$）：

其中核心点E由核心点A密度直达，

边界点B由核心点A密度可达，

边界点B与边界点C密度相连，

N为孤单的噪声点。

DBSCAN是基于密度的聚类算法，原理为：只要任意两个样本点是密度直达或密度可达的关系，那么该两个样本点归为同一簇类，上图的样本点ABCE为同一簇类。因此，DBSCAN算法从数据集D中随机选择一个核心点作为“种子”，由该种子出发确定相应的聚类簇，当遍历完所有核心点时，算法结束。

DBSCAN算法的伪代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# DB为数据集，distFunc为样本间的距离函数
# eps为样本点的领域，MinPts为簇类的最小样本数
DBSCAN(DB,distFunc,eps,minPts){
    C = 0                                           # 初始化簇类个数
    # 数据集DB被标记为核心点和噪声点
    for each point P in database DB{                #  遍历数据集 
        if label(P) != undefined then continue     # 如果样本已经被标记了，跳过此次循环
        Neighbors N = RangeQuery(DB,distFunc,P,eps)  # 计算样本点P在eps邻域内的个数，包含样本点本身
        if |N| < minPts then {                      # 密度估计
            label(P) = Noise                         # 若样本点P的eps邻域内个数小于MinPts，则为噪声
            continue
        }
        C = C + 1              # 增加簇类个数
        label(P) = C           # 初始化簇类标记
        Seed set S = N \{P}    # 初始化种子集，符号\表示取补集
        for each point Q in S{
            if label(Q) = Noise then label(Q) = C   # 核心点P的邻域为噪声点，则该噪声点重新标记为边界点
            if label(Q) != undefined then continue  # 如果样本已经被标记了(如上次已经被标记的噪声)，跳过此次循环
            label(Q) = C                    # 核心点P的邻域都标记为簇类C
            Neighbors N = RangeQuery(DB,distFunc,Q,eps)  # 计算样本Q的邻域个数
            if N >= minPts then{                        # 密度检测，检测Q是否为核心样本
                S = S.append(N)                # 邻域Q样本添加到种子集
            }
        }
    }
}
其中计算样本Q邻域个数的伪代码：

# 计算样本Q的eps邻域集
RangeQuery(DB,distFunc,Q,eps){
    Neighbors = empty list  # 初始化Q样本的邻域为空集
    for each point P in database DB{
        if distFunc(Q,P) <= eps then {
            Neighbors = Neighbors.append(Q)   # 若Q在P的eps邻域内，则邻域集增加该样本
        }
    }
    return Neighbors
}

其中计算样本P与Q的距离函数dist(P,Q)不同，邻域形状也不同，若我们使用的距离是曼哈顿（manhattan）距离，则邻域性状为矩形；若使用的距离是欧拉距离，则邻域形状为圆形。

DBSCAN算法可以抽象为以下几步：

1）找到每个样本的 $\varepsilon-$ 邻域内的样本个数，若个数大于等于$MinPts$，则该样本为核心点；

2）找到每个核心样本密度直达和密度可达的样本，且该样本亦为核心样本，忽略所有的非核心样本；

3）若非核心样本在核心样本的 $\varepsilon-$ 邻域内，则非核心样本为边界样本，反之为噪声。

DBSCAN的参数估计

$\varepsilon$ ：两个样本的最小距离，它的含义为：如果两个样本的距离小于或等于值 $\varepsilon$ ，那么这两个样本互为邻域。

$MinPts$：形成簇类所需的最小样本个数，比如$MinPts$等于5，形成簇类的前提是至少有一个样本的 $\varepsilon-$ 邻域大于等于5。

$\varepsilon$ 参数和 $MinPts$ 参数估计：

如下图，如果 $\varepsilon$ 值取的太小，部分样本误认为是噪声点（白色）； $\varepsilon$ 值取的过大，大部分的样本会合并为同一簇类。

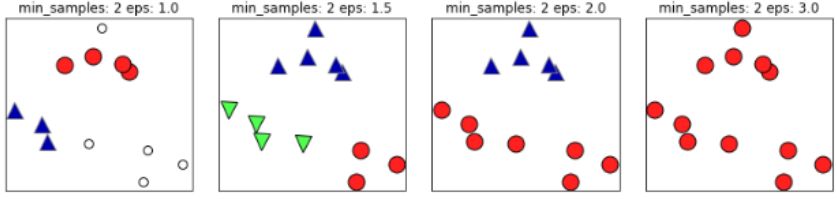
同样的，若$MinPts$值过小，则所有样本都可能为核心样本；$MinPts$值过大时，部分样本误认为是噪声点（白色），如下图：

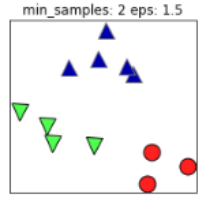
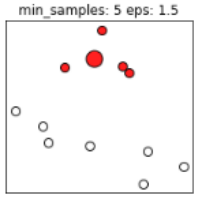
根据经验，$MinPts$ 的最小值可以从数据集的维数 $D$ 得到，即 $MinPts>=D+1$ 。若 $MinPts=1$，含义为所有的数据集样本都为核心样本，即每个样本都是一个簇类；若$MinPts \leq 2$，结果和单连接的层次聚类相同；因此 $MinPts$ 必须大于等于3，因此一般认为 $MinPts=2*ndims$ ，若数据集越大，则 $MinPts$ 的值选择的亦越大。

$\varepsilon$ 值常常用 $k-$ 距离曲线（k-distance graph）得到，计算每个样本与所有样本的距离，选择第k个最近邻的距离并从大到小排序，得到 $k-$ 距离曲线，曲线拐点对应的距离设置为 $\varepsilon$ ，如下图：

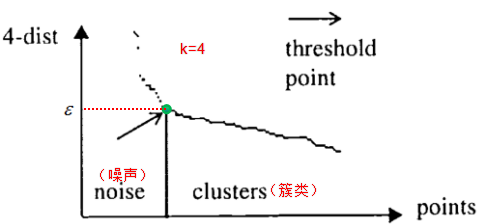
由图可知或者根据 $k-$ 距离曲线的定义可知：样本点第 $k$ 个近邻距离值小于 $\varepsilon$ 归为簇类，大于 $\varepsilon$ 的样本点归为噪声点。根据经验，一般选择 $\varepsilon$ 值等于第$（MinPts-1）$的距离，计算样本间的距离前需要对数据进行归一化，使所有特征值处于同一尺度范围，有利于 $\varepsilon$ 参数的设置。

如果 $(k+1)-$ 距离曲线和 $k-$ 距离曲线没有明显差异，那么 $MinPts$ 设置为k值。例如$k=4$和 $k>4$ 的距离曲线没有明显差异，而且 $k>4$ 的算法计算量大于 $k=4$ 的计算量，因此设置 $MinPts=4$ 。

DBSCAN算法实战

$k-means$ 聚类算法假设簇类所有方向是同等重要的，若遇到一些奇怪的形状（如对角线）时，k-means的聚类效果很差，本节采用DBSCAN算法以及简单的介绍下如何去选择参数 $\varepsilon$ 和 $MinPts$。

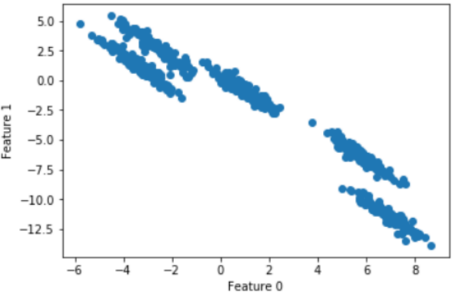
随机生成五个簇类的二维数据：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

# 生成随机簇类数据
X, y =make_blobs(random_state=170,n_samples=600,centers=5)
rng = np.random.RandomState(74)
# 数据拉伸
transformation = rng.normal(size=(2,2))
X = np.dot(X,transformation)
# 绘制延伸图
plt.scatter(X[:,0],X[:,1])
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

散点图为：

k-means聚类结果：

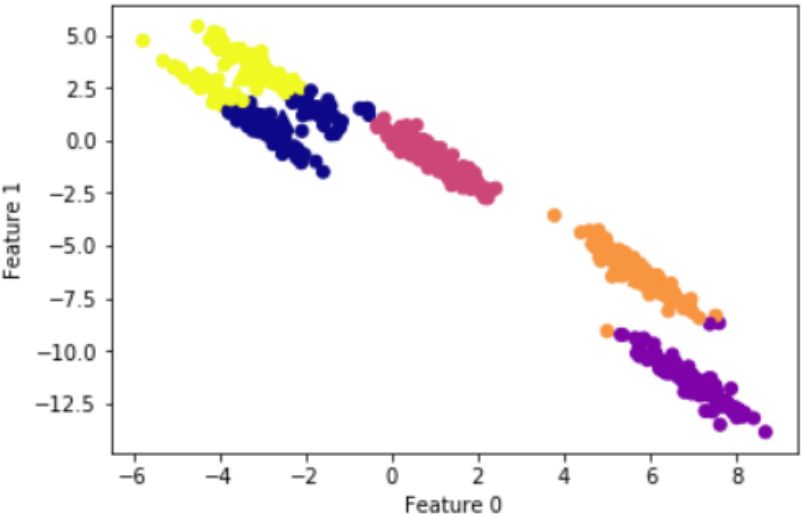
按照经验 $MinPts=2*ndims$，因此我们设置 $MinPts=4$ 。

为了方便参数 $\varepsilon$ 的选择，我们首先对数据的特征进行归一化：

1
2
3

#特征归一化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

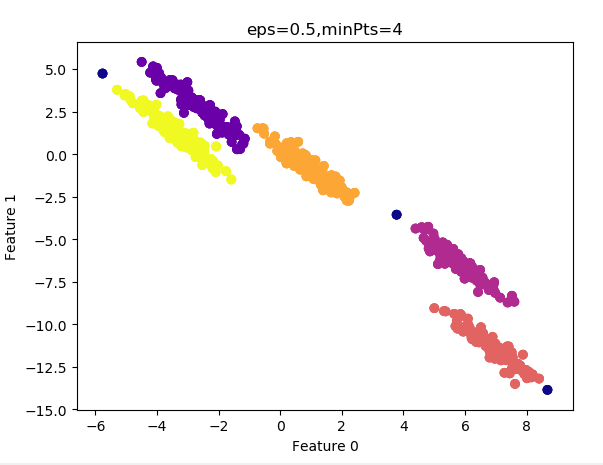
假设 $\varepsilon=0.5$ ：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

# dbscan聚类算法
t0=time.time()
dbscan = DBSCAN(eps=0.12,min_samples = 4)
clusters = dbscan.fit_predict(X_scaled)
# 绘制dbscan聚类结果
plt.scatter(X[:,0],X[:,1],c=clusters,cmap="plasma")
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.title("eps=0.5,minPts=4")
plt.show()
t1=time.time()
print(t1-t0)

查看聚类结果：

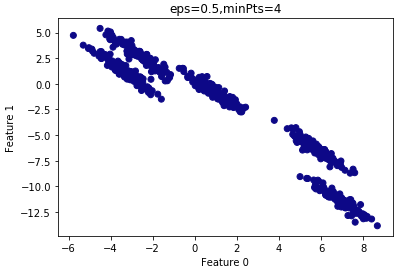
由上图可知，所有的样本都归为一类，因此 $\varepsilon$ 设置的过大，需要减小 $\varepsilon$ 。

设置 $\varepsilon=0.2$ 的结果：

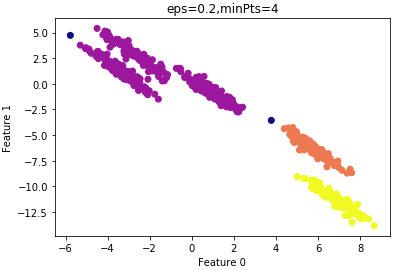
由上图可知，大部分样本还是归为一类，还是 $\varepsilon$ 设置的过大，仍需要减小 $\varepsilon$

设置 $\varepsilon=0.12$ 的结果：

结果令人满意，看看聚类性能度量指数：

1
2
3
4
5
6

# 性能评价指标ARI
from sklearn.metrics.cluster import adjusted_rand_score
# ARI指数
print("ARI=",round(adjusted_rand_score(y,clusters),2))

ARI= 0.99

由上节可知，为了较少算法的计算量，我们尝试减小 $MinPts$ 的值。 设置$MinPts=2$ 的结果：

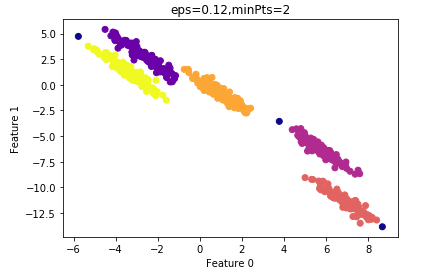
其ARI指数为：0.99

算法的运行时间较 $ MinPts=4$ 时要短，因此我们最终选择的参数： $\varepsilon=0.12$ ，$MinPts=2$。

这是一个根据经验的参数优化算法，实际项目中，我们首先根据先验经验去设置参数的值，确定参数的大致范围，然后根据性能度量去选择最优参数。

DBSCAN算法的优缺点

优点：

1、DBSCAN不需要指定簇类的数量；

2、DBSCAN可以处理任意形状的簇类；

3、DBSCAN可以检测数据集的噪声，且对数据集中的异常点不敏感；

4、DBSCAN结果对数据集样本的随机抽样顺序不敏感（细心的读者会发现样本的顺序不一样，结果也可能不一样，如非核心点处于两个聚类的边界，若核心点抽样顺序不同，非核心点归于不同的簇类）；

缺点：

1、DBSCAN最常用的距离度量为欧式距离，对于高维数据集，会带来维度灾难，导致选择合适的 $\varepsilon$ 值很难；

2、若不同簇类的样本集密度相差很大，则DBSCAN的聚类效果很差，因为这类数据集导致选择合适的 $MinPts$ 和 $\varepsilon$ 值非常难，很难适用于所有簇类.