CNN

CNN（卷积【对两个实变函数的一种数学运算】神经网络）主要由两部分组成：

1、特征提取（卷积、激活函数、池化）【从概率分布的视角看(bayes派)这是一种无限强的先验（这个先验说明了该层应该学得的函数只包含局部连接关系并且对平移具有等变性）】

先验被认为是强或者弱取决于先验中概率密度的集中程度：

  • 弱先验具有较高的熵值，例如方差很大的高斯分布。这样的先验允许数据对于参数的改变具有较大的自由性；
  • 强先验具有较低的熵值，例如方差很小的高斯分布。这样的先验在决定参数时，对最终取值时起着更大的决定性作用

2、分类识别（全连接）

两层之间所有神经元都有权重连接，通常全连接层在卷积神经网络尾部。也就是跟传统的神经网络神经元的连接方式一样

CNN详解

卷积理解

卷积本质是加权叠加，意义是对信号进行滤波

连续卷积 $\displaystyle \int^{\infty}_{-\infty} f(\tau)g(x-\tau)d\tau$

离散卷积 $\displaystyle \sum^{\infty}_{\tau=-\infty} f(\tau)g(x-\tau)$

从公式上来看我们进行了三步操作：

1、我们对 $g$ 函数沿着y轴翻转了180°

2、把翻转后的 $g$ 函数平移n在这个位置

3、对处理后的 $g$ 函数和 $f$ 的对应点相乘求和

翻转和平移都是为了对应相乘求积分

例如求两粒骰子加起来等于4的概率是多少就是一个典型的离散卷积

那么我们的做法是假设第一粒骰子符合离散函数 $f$ 第二粒骰子符合离散函数 $g$ 那么两粒骰子加起来等于4的概率可以表示为 $f(1)g(3)+f(2)g(2)+ f(3)g(1)$

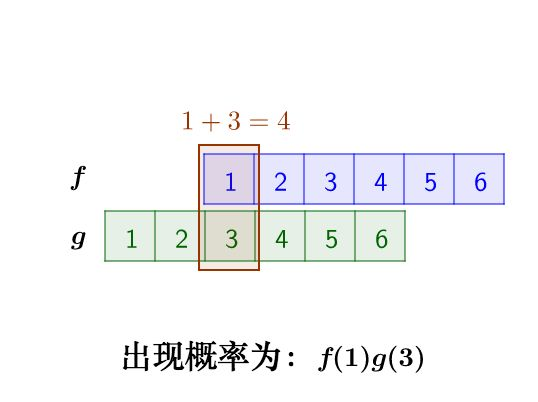
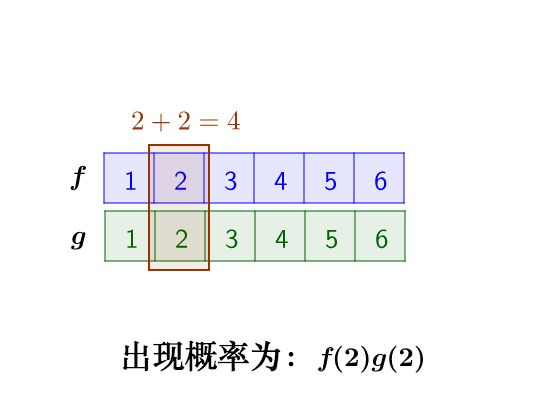
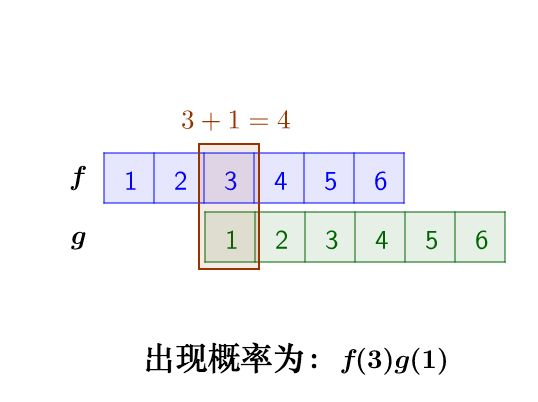
对函数 $g$ 进行翻转平移可以得到 $f(1)g(3)+f(2)g(2)+ f(3)g(1) = f(1)g(4-1)+f(2)g(4-2)+f(3)g(4-1)$

其对应的图为：

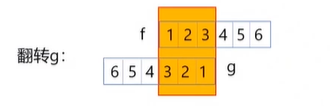
二维层面的卷积如下：

求新的某一个卷积值例如 $c_{1,1}$

在图中的展现形式为：

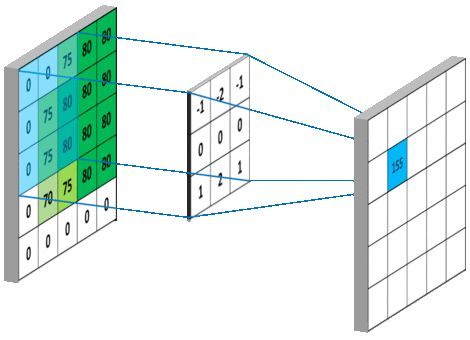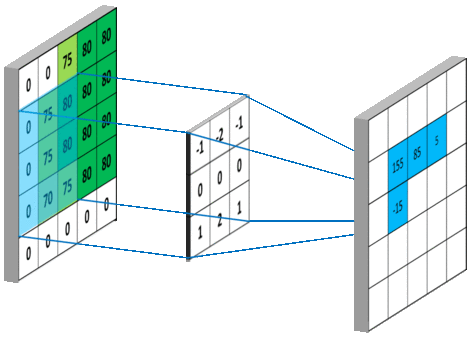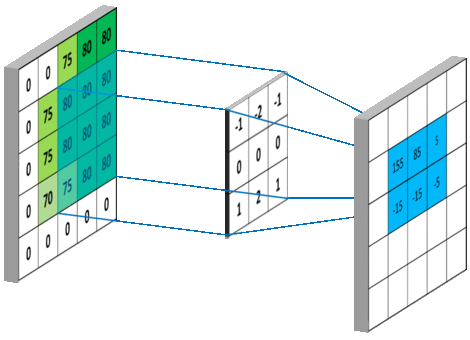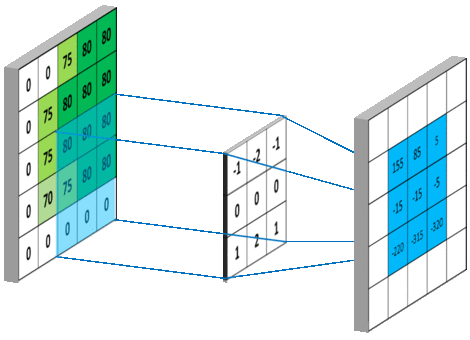
在tensorflow中padding的值可以设为SAME、VALID分别是对卷积方式的控制

SAME卷积方式指在卷积核的核心k从原矩阵第一个值开始平滑(当步长为1时，卷积后的矩阵尺寸等于原矩阵大小)：

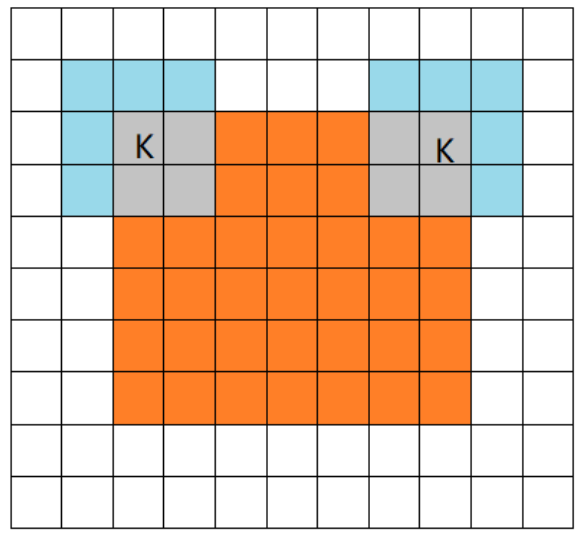
VALID卷积方式指在卷积核完全从原矩阵内开始卷积(无论步长设为多少，卷积后的矩阵尺寸小于原矩阵)：

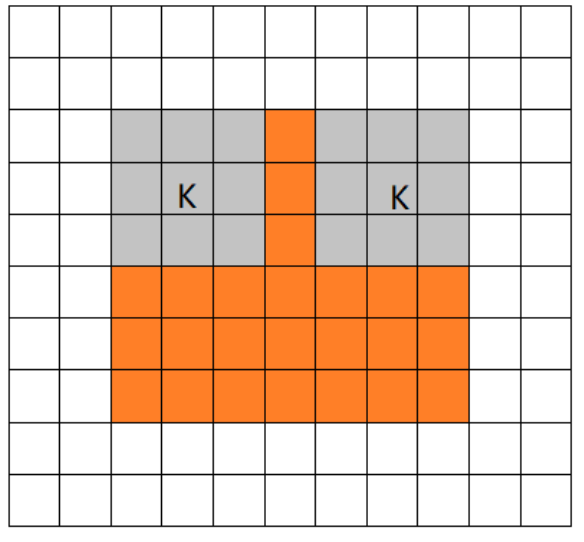
当我们使用多个卷积核时对三维数据进行处理时如下：

采用的方式为same、步长为2

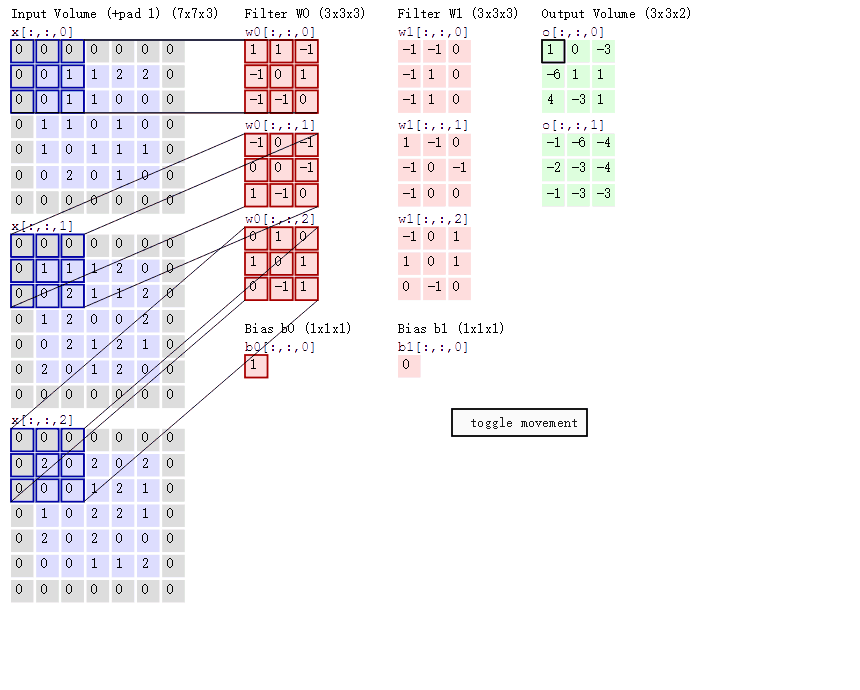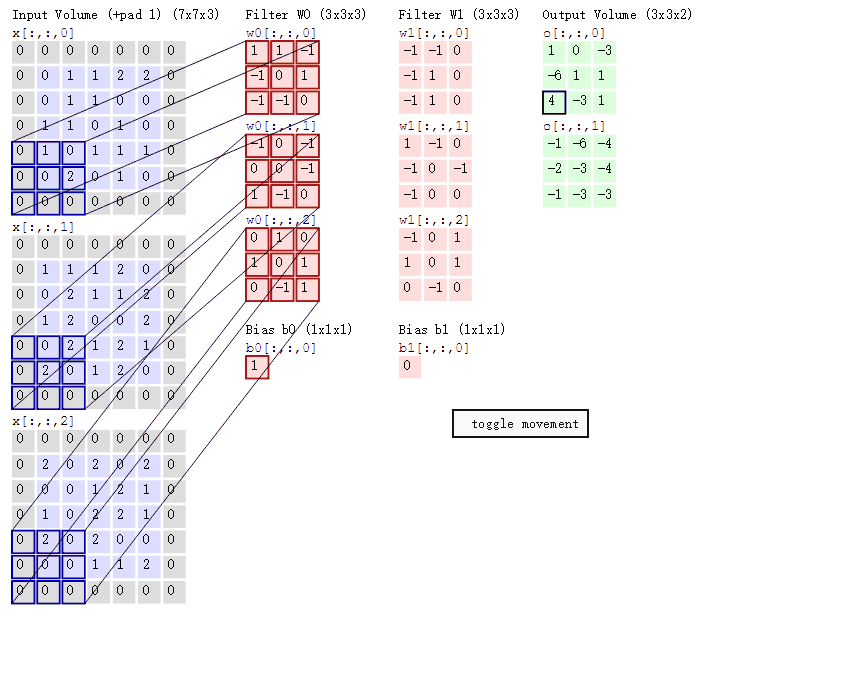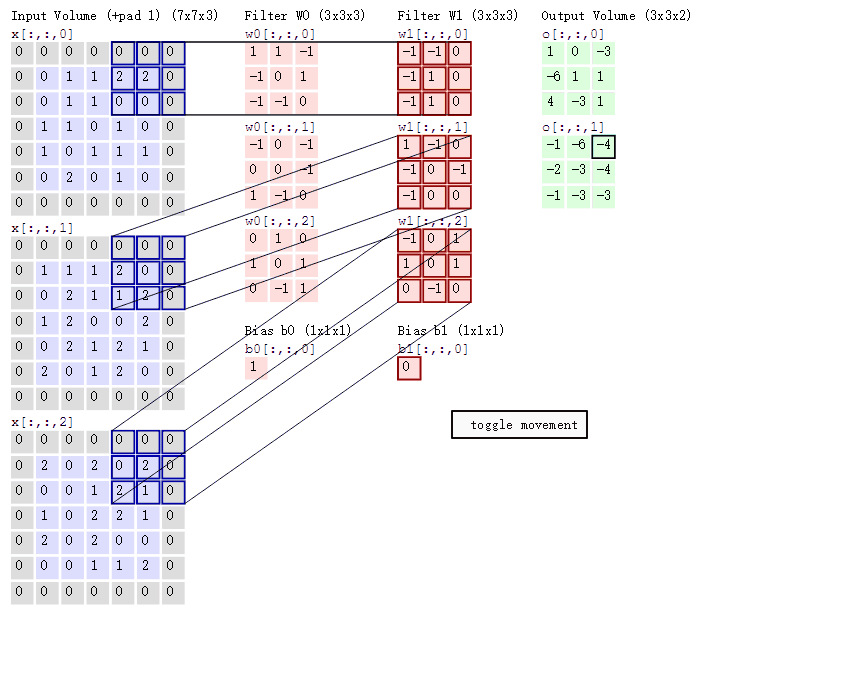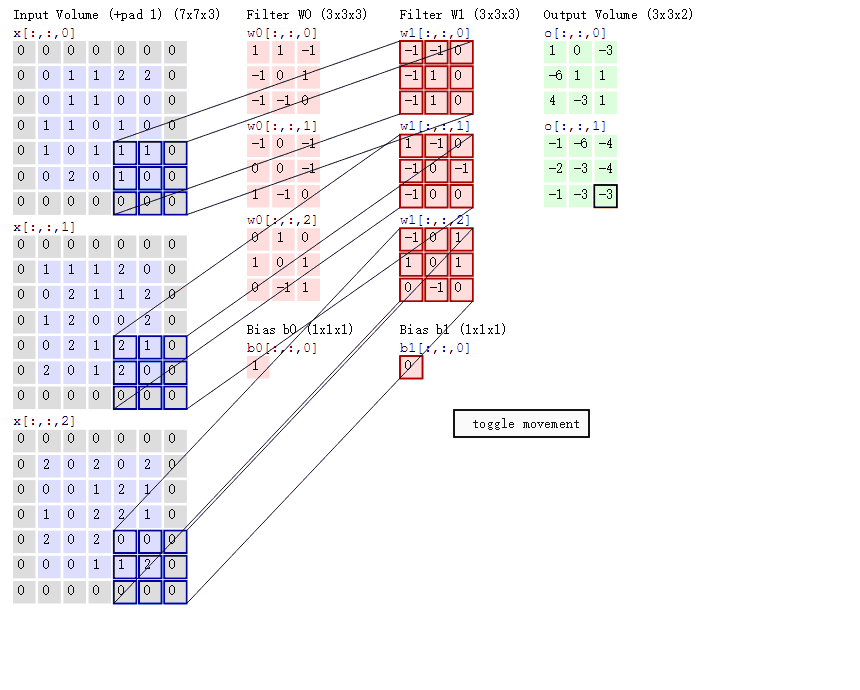
通过上述探究可知same方式输出矩阵与输入矩阵的尺寸关系： $n_{输出矩阵尺寸} = 向上取整( \displaystyle \frac{n_{输入矩阵尺寸}}{S_{步长}})$

valid方式输出矩阵与输入矩阵的尺寸关系： $n_{输出矩阵尺寸} = 向上取整( \displaystyle \frac{n_{输入矩阵尺寸}-f_{卷积核尺寸}+1}{S_{步长}})$

卷积的意义

以边缘检测卷积为例子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# talk is cheap show me the code

# -*-* encoding:UTF-8 -*-
# python3
# author : DK
# date   : 2022/03/02

import requests
import numpy as np
from PIL import Image
from io import BytesIO
from scipy import signal # 支持二维卷积


# 图片地址
url = 'http://p6-bk.byteimg.com/tos-cn-i-mlhdmxsy5m/0e8f58a29b894fdaafaa957d75a96ca9~tplv-mlhdmxsy5m-q75:0:0.image'
response = requests.get(url)
pic = Image.open(BytesIO(response.content))
data = np.array(pic)
print("图片矩阵的维度：", data.shape)

# 定义卷积核，边缘识别
k = np.array([[-1, 0, 1], 
              [-2, 0, 2], 
              [-1, 0, 1]])

df = []
for i in range(data.shape[2]):
    value = signal.convolve2d(data[:, :, i], k, 'same')
    # 过滤杂质，类似于激活函数relu
    value[value < 0] = 0
    df.append(value)
    
pic_df = np.dstack(df) #深度叠加，扩维

# 还原图片
pic_new = Image.fromarray(np.uint8(pic_df))
pic_new.show()

边缘效果如下：

最后cnn神经网络在学习之后学到的卷积核就类似于这种，能体现图片一部分特征

卷积核的选择

常见的卷积核多为奇数

  1. 奇数相对于偶数，有中心点，对边沿、对线条更加敏感，可以更有效的提取边沿信息;
  2. 如果卷积核size是奇数，就可以从图像的两边对称的padding;
  3. 奇数size的卷积核，有central pixel 可以方便的确定position;

参数共享

参数共享的目的很简单就是通过降低参数量减少计算量

1、局部连接（卷积核通常采用3*3或5*5）

对一个边长为10的矩阵进行全连接卷积，如果输出矩阵的大小要求相同，那么需要参数的数量为

$10*10_{单个全连接卷积核大小}*(10*10)_{保持原输入矩阵大小}$

如果采用局部链接例如3*3矩阵，如果输出矩阵的大小要求相同，那么需要的参数数量为：

$3*3_{单个卷积核大小}*(10*10)_{保持原输入矩阵大小}$

2、在一个卷积核（滤波器）平滑的过程中，原数据共享一个卷积核参数

即只是卷积核大小+偏置数

能采用参数共享的依据是：

1、局部连接有效是因为局部视野可以反馈原始数据特征

2、单个卷积核(滤波器)就是一个特征映射，增加卷积核个数即可增加特征维度

激励函数

本质上的神经网络是矩阵运算，其核心是线性的，采用激活函数可以解决线性不能解决的问题

池化理解(下采样)

在卷积后的特征上，单个区域内的值可以被其均值或最大值替代，在生活中常见的就是像素画，如下：

池化的意义：

1、保留主要特征的同时减少参数（降低纬度，类似PCA）和计算量，防止过拟合

2、invariance(不变性)，这种不变性包括translation(平移)，rotation(旋转)，scale(尺度，尺寸问题)

3、减少网络参数个数

池化的实现过程，以最大池化为例：

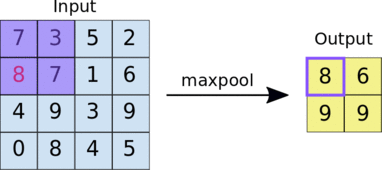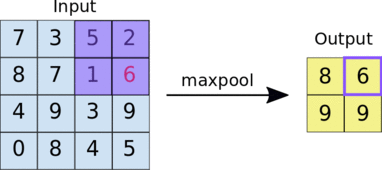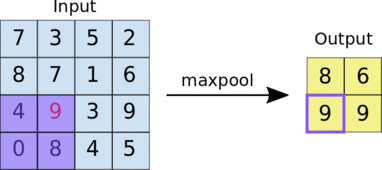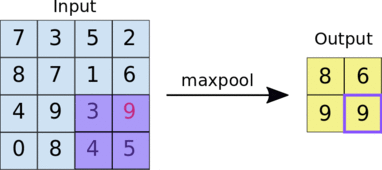
全连接层

特征拍扁，多维度特征映射到同一个维度

全连接层在整个网络卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话（特征提取+选择的过程），全连接层则起到将学到的特征表示映射到样本的标记空间的作用。换句话说，就是把特征整合到一起（高度提纯特征），方便交给最后的分类器或者回归。

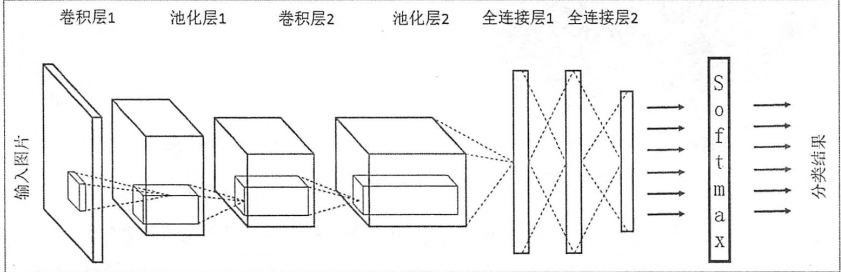
dropout

dropout强迫一个神经单元，和随机挑选出来的其他神经单元共同工作，达到好的效果。消除减弱了神经元节点间的联合适应性，增强了泛化能力。

对大数据量而言，当dropout=0.5时，信息熵最大，dropout随机生成的网络结构最多，所以理论上效果最好

CNN的简单使用

使用tensorflow1.15版本

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139

import gc
import warnings
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

warnings.filterwarnings("ignore")

# 数据获取，方法2
data = np.load('/data/datas/mnist.npz')
print(data.files)
# 随机取batch_size个训练样本
def next_batch(train_data, train_target, batch_size):
    index = [ i for i in range(0,len(train_target)) ]
    np.random.shuffle(index);
    batch_data = [];
    batch_target = [];
    for i in range(0,batch_size):
        batch_data.append(train_data[index[i]]);
        batch_target.append(train_target[index[i]])
    return batch_data, batch_target
x_train = data['x_train'].reshape(60000,784)/255
y_train = np.eye(10)[data['y_train']]
x_test = data['x_test'].reshape(10000,784)/255
y_test = np.eye(10)[data['y_test']]
# 释放数据
del data
gc.collect()

#创建一个交互式Session
sess = tf.InteractiveSession()
 
#创建两个占位符，x为输入网络的图像，y_为输入网络的图像类别
x = tf.placeholder("float", shape=[None, 784])
y_ = tf.placeholder("float", shape=[None, 10])
#权重初始化函数
def weight_variable(shape):
    #输出服从截尾正态分布的随机值
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)
 
#偏置初始化函数
def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)
 
#创建卷积op
#x 是一个4维张量，shape为[batch,height,width,channels]
#卷积核移动步长为1。填充类型为SAME,可以不丢弃任何像素点
def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1,1,1,1], padding="SAME")
 
#创建池化op
#采用最大池化，也就是取窗口中的最大值作为结果
#x 是一个4维张量，shape为[batch,height,width,channels]
#ksize表示pool窗口大小为2x2,也就是高2，宽2
#strides，表示在height和width维度上的步长都为2
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1,2,2,1],
                          strides=[1,2,2,1], padding="SAME")
 
 
#第1层，卷积层
#初始化W为[5,5,1,32]的张量，表示卷积核大小为5*5，第一层网络的输入和输出神经元个数分别为1和32
W_conv1 = weight_variable([5,5,1,32])
#初始化b为[32],即输出大小
b_conv1 = bias_variable([32])
 
#把输入x(二维张量,shape为[batch, 784])变成4d的x_image，x_image的shape应该是[batch,28,28,1]
#-1表示自动推测这个维度的size
x_image = tf.reshape(x, [-1,28,28,1])
 
#把x_image和权重进行卷积，加上偏置项，然后应用ReLU激活函数，最后进行max_pooling
#h_pool1的输出即为第一层网络输出，shape为[batch,14,14,1]
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
 
#第2层，卷积层
#卷积核大小依然是5*5，这层的输入和输出神经元个数为32和64
W_conv2 = weight_variable([5,5,32,64])
b_conv2 = weight_variable([64])
 
#h_pool2即为第二层网络输出，shape为[batch,7,7,1]
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
 
#第3层, 全连接层
#这层是拥有1024个神经元的全连接层
#W的第1维size为7*7*64，7*7是h_pool2输出的size，64是第2层输出神经元个数
W_fc1 = weight_variable([7*7*64, 1024])
b_fc1 = bias_variable([1024])
 
#计算前需要把第2层的输出reshape成[batch, 7*7*64]的张量
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
 
#Dropout层
#为了减少过拟合，在输出层前加入dropout
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, rate = 1-keep_prob)
 
#输出层
#最后，添加一个softmax层
#可以理解为另一个全连接层，只不过输出时使用softmax将网络输出值转换成了概率
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
 
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
 
#预测值和真实值之间的交叉墒
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
 
#train op, 使用ADAM优化器来做梯度下降。学习率为0.0001
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
 
#评估模型，tf.argmax能给出某个tensor对象在某一维上数据最大值的索引。
#因为标签是由0,1组成了one-hot vector，返回的索引就是数值为1的位置
correct_predict = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
 
#计算正确预测项的比例，因为tf.equal返回的是布尔值，
#使用tf.cast把布尔值转换成浮点数，然后用tf.reduce_mean求平均值
accuracy = tf.reduce_mean(tf.cast(correct_predict, "float"))
 
#初始化变量
sess.run(tf.global_variables_initializer())
 
#开始训练模型，循环20000次，每次随机从训练集中抓取50幅图像
for i in range(101):
    # batch = mnist.train.next_batch(50)
    batch = next_batch(x_train,y_train,100)
    if i%100 == 0:
        #每100次输出一次日志
        train_accuracy = accuracy.eval(feed_dict={x:batch[0], y_:batch[1], keep_prob:1.0})
        print("step %d, training accuracy %g" % (i, train_accuracy))
    train_step.run(feed_dict={x:batch[0], y_:batch[1], keep_prob:0.5})
 
# print("test accuracy %g" % accuracy.eval(feed_dict={x:mnist.test.images, y_:mnist.test.labels, keep_prob:1.0}))
print("test accuracy %g" % accuracy.eval(feed_dict={x:x_test[:100,:], y_:y_test[:100,:], keep_prob:1.0}))

反向传播推导

CNN的优缺点

优点

1、共享卷积核，可以轻松处理高维数据

2、自动进行特征提取器参数学习

缺点

1、cnn没有记忆功能

2、cnn特征检测能力很强，但是特征理解能力很差

参考：

卷积理解

卷积总结

卷积原理

反向传播

实现卷积