文本表示(二)
文章目录
文本表示(二)
文本表示的意思是把字词处理成向量或矩阵,以便计算机能进行处理。
文本表示按照细粒度可划分:字级别、词语级别、句子级别的文本表示。
文本表示可以分为两大类:
- 离散表示(特征:离散、高维、稀疏):one-hot、BOW、TF-IDF、n-gram
- 分布式表示(特征:连续、低维、稠密):word2vec、Glove、ELMO、GPT、BERT。
NNLM原理
想法:把单词映射为一个具有一定维度的实数向量,每一个词都和一个特征向量相关联。
做法:由于自然语言天然就有逻辑性,可设定任务根据$w_{t−n+1}…w_{t−1}$ 来预测 $w_{t}$ 是什么词,即用 $n−1$ 个单词来预测第 $n$ 个词
实现方法:
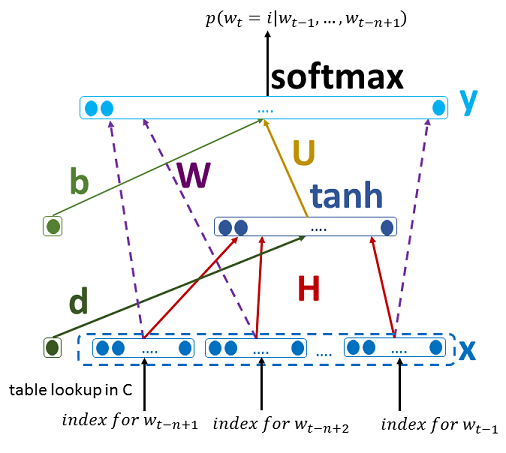
观察上图,假设有一组词序列:$w_{t-n+1}, w_{t-n+2},···,w_{t-1}$ ,其中 $w_i \in V$ , $V$ 是所有单词的集合。我们的输入是一个词序列,而我们的输出是一个概率值,表示根据 $w_{t-n+1}, w_{t-n+2},···,w_{t-1}$ 预测出下一个词是 $i$ 的概率。用数学来表示,我们最终是要训练一个模型:
$f(w_t,w_{t-1},···,w_{t-n+1}) = P(w_t=i|w_{t-1},···w_{t-n+1}) = P(w_t|w_1^{t-1})$
其中有:
- $w_t$ 表示这个词序列中的第 $t$ 个单词, $w_{t-n+1}$ 表示输入长度为 $n$ 的词序列中的第一个单词
- $w_1^{t-1}$ 表示从第1个单词到第 $t-1$ 个单词组成的子序列
我们发现, 这个过程与上面提到的其实是一样的, 其实就是求: $p(w_n|w_1,···,w_{n-1})$
该模型需要满足两个约束条件:
所有概率大于零 $f(w_t,w_{t-1},···,w_{t-n+2},w_{t-n+1})>0$
所有概率和为1 $\displaystyle \sum_{i=1}^{|V|}{f(i,w_{t-1},···,w_{t-n+2},w_{t-n+1})} = 1$
其中 $|V|$ 表示词表的大小
具体做法可分为四步:
1、将one-hot矩阵通过矩阵(初始为随机生成,后续反向传播修正为合适矩阵)映射为m维向量,因为每一个词是m维的,总共有n-1个词,所以总共有 $(n−1)m$ 维(单个输入)
2、计算隐藏层 $h=tanh(H*x+d)$
3、计算输出层 $y = b+W*x +U*tanh(d+H*x)$

其中 $W$ 矩阵可以为0,当 $W!=0$ 时表示存在由输入直接到输出的连接,该连接可有可无,当存在时相当于扩展了基本特征
4、使用softmax函数归一化(反向传播这里不做推导):
$P = \displaystyle \frac{e^y}{\displaystyle\sum_{i=1}^{n}e^{y_i}}$
word2Vec
CBOW(Continuous Bag of Words)
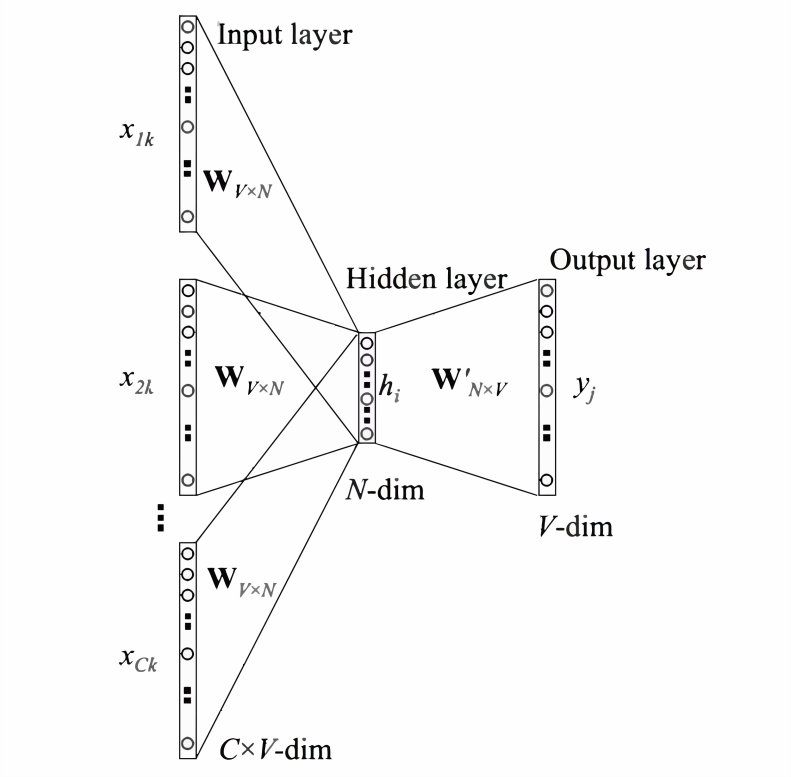
CBOW模型的应用场景是要根据上下文预测中间词,所以我们的输入便是上下文词,当然原始的单词是无法作为输入的,这里的输入仍然是每个词汇的one-hot向量,输出为给定词汇表中每个词作为目标词的概率。
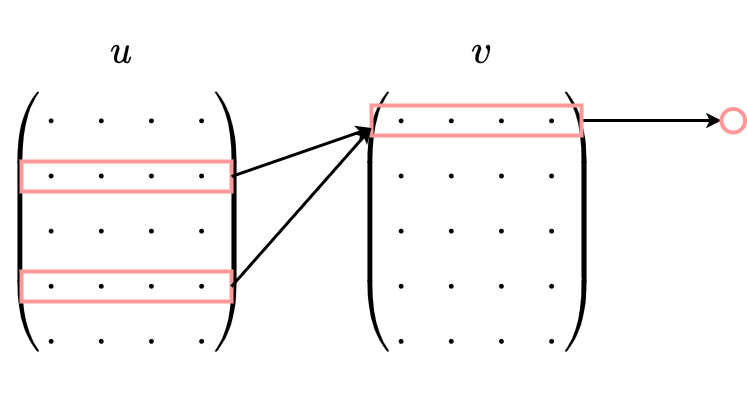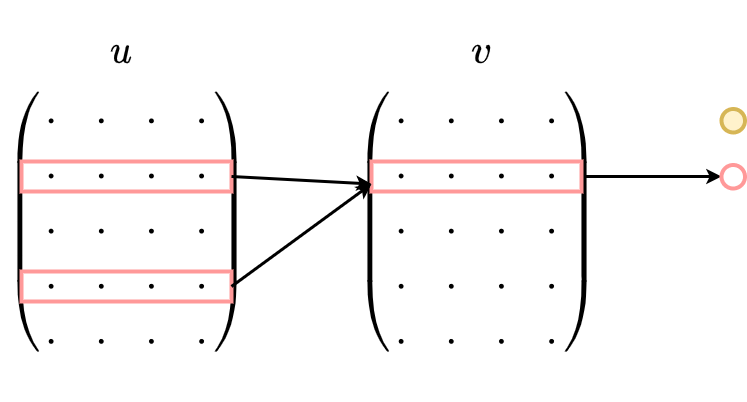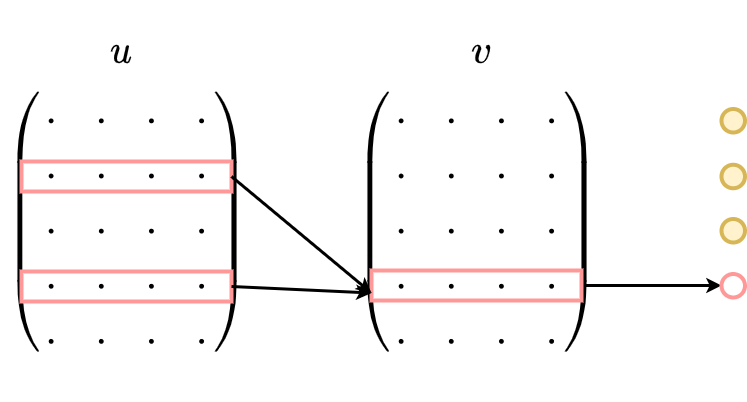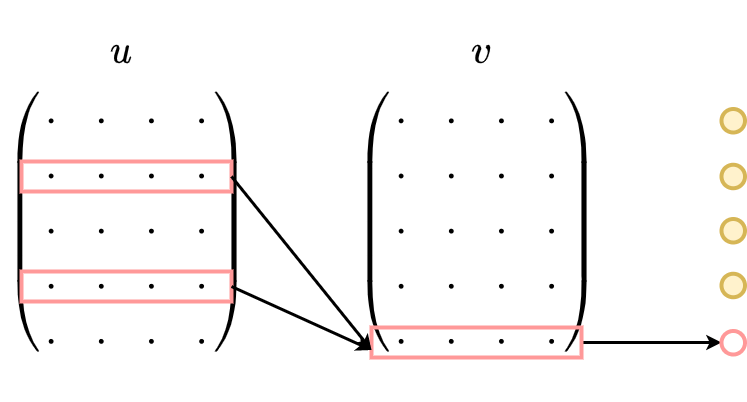
1、CBOW没有隐藏层,本质上只有两层结构,输入层将目标词语境 $C$ 中的每一个词向量简单求和(当然,也可以求平均)后得到语境向量
2、然后直接与目标词的输出向量求点积,目标函数也就是要让这个与目标词向量的点积取得最大值,对应的与非目标词的点积尽量取得最小值。
需要注意的是这里每个词对应到两个词向量,在上面的公式中都有体现,其中 $e(w_t)$ 是词的输入向量,而 $e′(w_t)$ 则是词的输出向量,或者更准确的来讲,前者是CBOW输入层中跟词 $w_t$ 所在位置相连的所有边的权值(其实这就是词向量)组合成的向量,而是输出层中与词 $w_t$ 所在位置相连的所有边的权值组合成的向量,所以把这一向量叫做输出向量。
优点:
1、CBOW取消了NNLM中的隐藏层,直接将输入层和输出层相连;
2、在求语境context向量时候,语境内的词序已经丢弃(这个是名字中Continuous的来源);
3、最终的目标函数仍然是语言模型的目标函数,所以需要顺序遍历语料中的每一个词(这个是名字中Bag-of-Words的来源)
4、将特征词嵌入上下文环境
5、后续还在训练方法上进行了优化:层次softmax以及负采样技术
Skip-gram
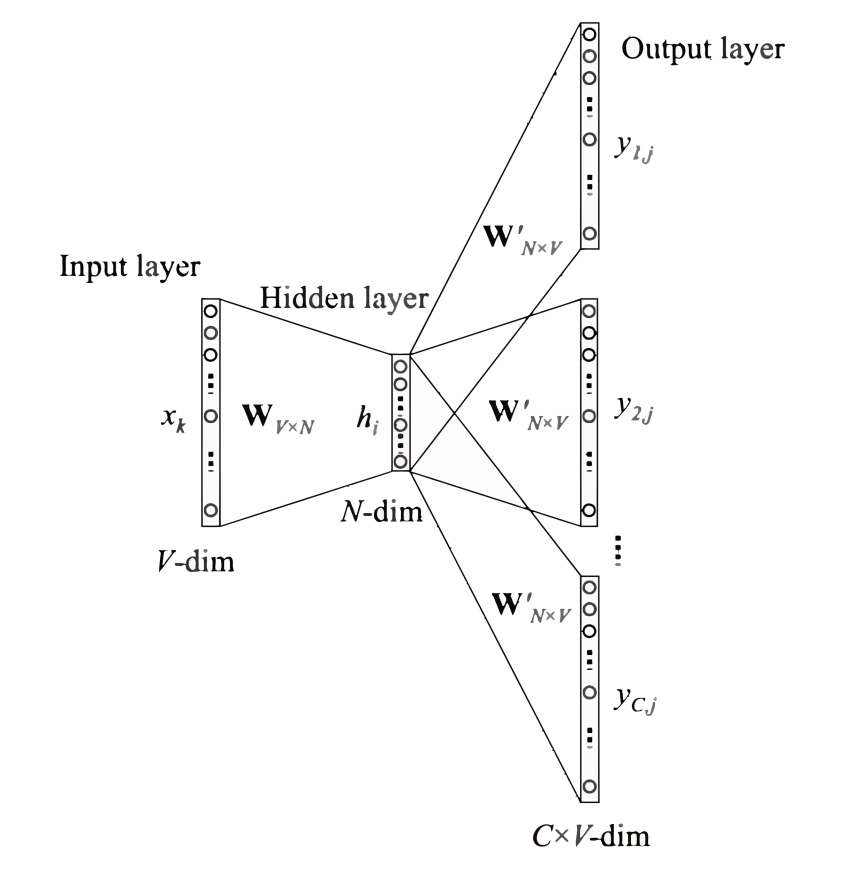
Skip-gram模型的应用场景是要根据中间词预测上下文词(比较适用于大数据),所以我们的输入是任意单词,输出为给定词汇表中每个词作为上下文词的概率。
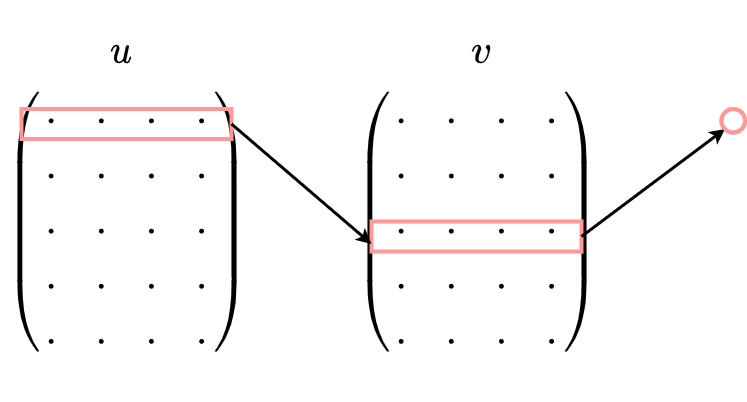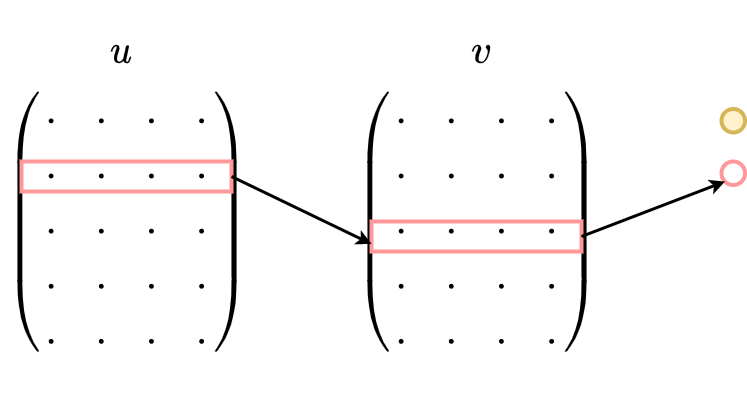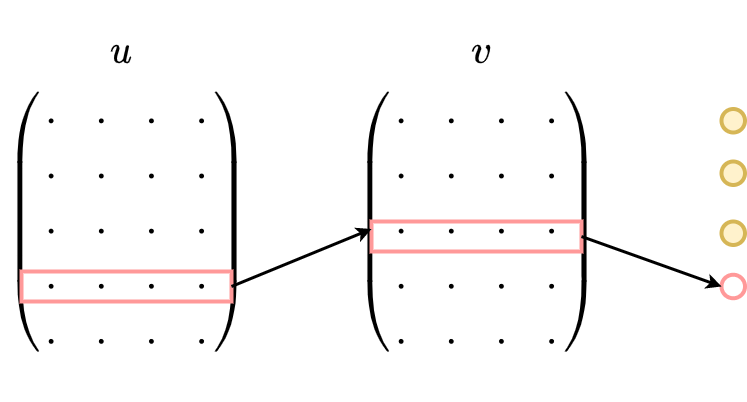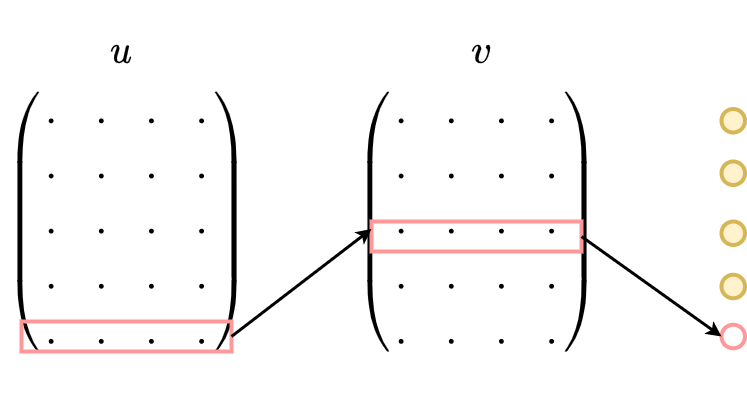
Skip-gram本质上也只有两层:输入层和输出层,输入层负责将输入词映射为一个词向量,输出层负责将其经过线性映射计算得到每个词的概率大小。再细心一点的话,其实无论CBOW还是Skip-gram,本质上都是两个全连接层的相连,中间没有 任何其他的层。因此,这两个模型的参数个数都是 $2*|e|*|V|$,其中 $|e|$ 和 $|V|$ 分别是词向量的维度和词典的大小,相比上文中我们计算得到NNLM的参数个数 $|V|(1+|H|+|e|n)+|H|(1+|e|n-|e|)$ 已经大大减小,且与上下文所取词的个数无关了
缺点:
1、由于词和向量是一对一的关系,所以多义词的问题无法解决。
2、Word2vec 是一种静态的方式,虽然通用性强,但是无法针对特定任务做动态优化
文章作者 玉面蟾蜍
上次更新 2022-03-12 Sat
